Answer:
12.649
Skills needed: Trigonometry
Explanation:
1) We need to use one of the fundamentals of trigonometry, which is:
Soh Cah Toa
---> Soh =
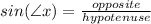 (
(
 equals the side Opposite of it divided by the Hypotenuse -- sin is short for sine (pronounced as sign)
equals the side Opposite of it divided by the Hypotenuse -- sin is short for sine (pronounced as sign)
Soh = Sine Opposite Hypotenuse
---> Cah =
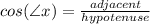 (
(
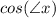 equals the side adjacent (not the hypotenuse) to the angle divided by the hypotenuse -- cos is short for cosine (pronounced as co-sign)
equals the side adjacent (not the hypotenuse) to the angle divided by the hypotenuse -- cos is short for cosine (pronounced as co-sign)
Cah = Cosine Adjacent Hypotenuse
---> Tan =
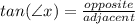 (
(
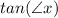 equals the side opposite of it divided by the side (not hypotenuse) adjacent to it -- tan is short for tangent
equals the side opposite of it divided by the side (not hypotenuse) adjacent to it -- tan is short for tangent
Tan = Tangent Opposite Adjacent
2) In this case, we are solving for adjacent:
This is because
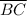 is next to
is next to
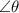 and
and
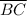 is not the hypotenuse (
is not the hypotenuse (
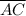 is the hypotenuse as it is opposite the right angle)
is the hypotenuse as it is opposite the right angle)
---> We are given opposite as side
 is opposite
is opposite
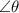
3) Let's plug it in:
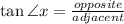

 --> Here, we should multiply both sides by
--> Here, we should multiply both sides by
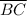
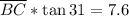 --> To get
--> To get
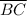 by itself, divide both sides by
by itself, divide both sides by

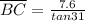
You have to plug this into the calculator as you cannot mentally solve trig functions.
---> Plugging it into calc:
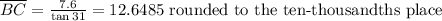
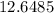 is rounded to the ten-thousandths, but the problem asks for 3 SF, so that would be
is rounded to the ten-thousandths, but the problem asks for 3 SF, so that would be
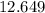 (rounded that 85 to 9 (or 90))
(rounded that 85 to 9 (or 90))