Question

Given f(x) = 10 - 16/x, find all c in the interval [2,8] that satisfy the mean value theorem

Answer 1

f(x)=10-16/x
f'(x)=16/x^2
f'(c)=16/c^2
f(8)=10-16/8=10-2=8
f(2)=10-16/2=10-8=2

`f'(c)= (f(b)-f(a))/(b-a) in (2,8), (16)/(c^2) = (f(8)-f(2))/(8-2) , (16)/(c^2) = (8-2)/(8-2)`
4∈[2,8] is the required point.

Answer 2

`c=4`

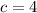
Explanation:

By defintion, the mean value theorem is

`f'(c)=(f(b)-f(a))/(b-a)`

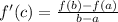
So, in this case, we know that
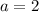`a=2` and
`b=8`.

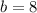Now, we need to find
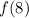`f(8)` and
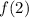`f(2)`, by replacing those values into the given function

`f(x)=10-(16)/(x)\\ f(8)=10-(16)/(8)=10-2=8`

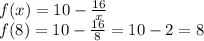
So,
`f(b)=f(8)=8`.

`f(x)=10-(16)/(x)\\ f(2)=10-(16)/(2)=10-8=2`

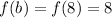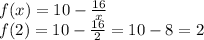
So,
`f(2)=2`

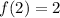
Then, we replace all values,

`f'(c)=(f(b)-f(a))/(b-a)=(8-2)/(8-2)=(6)/(6)=1`

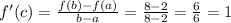
Now, we find the derivative of the function which has to be equal to one,

`f(x)=10-(16)/(x)=10-16x^(-1) \\f'(x)=16x^(-2) =(16)/(x^(2) ) =1`

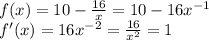
Now, we solve the equation to find the value c,

`(16)/(x^(2) ) =1\\x^(2) =16\\x=4`

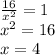
Therefore,
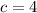`c=4` is the value inside the given interval that satisfy the mean value theorem.