Answer:
912
Explanation:
the assumption is that this is an arithmetic progression
the nth term of an arithmetic progression is
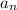 = a₁ + (n - 1)d
= a₁ + (n - 1)d
where a₁ is the first term and d the common difference
use this to find which term 120 is in the sequence
with a₁ = 32 and d = a₂ - a₁ = 40 - 32 = 8 , then
32 + 8(n - 1) = 120 ( subtract 32 from both sides )
8(n - 1) = 88 ( divide both sides by 8 )
n - 1 = 11 ( add 1 to both sides )
n = 12
given the first and last terms in the sequence then sum is
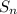 =
=
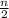 ( first + last)
( first + last)
S₁₂ =
 (32 + 120) = 6 × 152 = 912
(32 + 120) = 6 × 152 = 912