Question

Halp me plass halp me

Answer 1

The distance between AC is 15 units.

Explanation:

Here's the required formula to find distance between points A(2, 10) and C(14, 1) :

`{\implies{\small{\pmb{\sf{Distance = \sqrt{\Big(x_(2) - x_(1) \Big)^(2) + \Big(y_(2) - y_(1) \Big)^(2)}}}}}}`

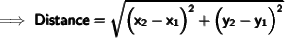
As per given question we have provided that :

`\begin{gathered}\begin{gathered} \footnotesize\rm {\underline{\underline{Where}}}\begin{cases}& \sf x_2 = 14\\ & \sf x_1 = 2\\ & \sf y_2 = 1\\& \sf y_1 = 10\end{cases} \end{gathered}\end{gathered}`

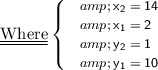
Substituting all the given values in the formula to find the distance between points A(2, 10) and C(14, 1) :

`\begin{gathered} \quad{\implies{\small{\sf{AC = \sqrt{\Big(x_(2) - x_(1) \Big)^(2) + \Big(y_(2) - y_(1) \Big)^(2)}}}}}\\\\\quad{\implies{\small{\sf{AC = \sqrt{\Big(14 - 2\Big)^(2) + \Big(1 - 10\Big)^(2)}}}}}\\\\\quad{\implies{\small{\sf{AC = \sqrt{\Big(\: 12 \:\Big)^(2) + \Big( - 9\Big)^(2)}}}}}\\\\ \quad{\implies{\small{\sf{AC = √(\Big(12 * 12\Big)+ \Big( - 9 * - 9\Big))}}}}\\\\\quad{\implies{\small{\sf{AC = √(\Big( \: 144 \: \Big)+ \Big( \: 81 \: \Big))}}}}\\\\ \quad{\implies{\small{\sf{AC = √(\Big(144 + 81\Big))}}}}\\\\\quad{\implies{\small{\sf{AC = √(\Big(225\Big))}}}}\\\\\quad{\implies{\small{\sf{\underline{\underline{\red{AC = 15}}}}}}} \end{gathered}`

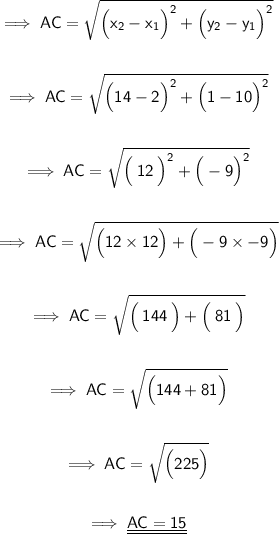
Hence, the distance between AC is 15 units.

`\rule{300}{2.5}`

Answer 2

`\displaystyle d = 15`

General Formulas and Concepts:

Pre-Algebra

Order of Operations: BPEMDAS

1. Brackets
2. Parenthesis
3. Exponents
4. Multiplication
5. Division
6. Addition
7. Subtraction

• Left to Right

Algebra I

Coordinate Planes

• Coordinates (x, y)

Algebra II

Distance Formula:
`\displaystyle d = √((x_2 - x_1)^2 + (y_2 - y_1)^2)`

Explanation:

Step 1: Define

Identify.

Point A(2, 10)

Point C(14, 1)

Step 2: Find distance d

Simply plug in the 2 coordinates into the distance formula to find distance d.

1. Substitute in points [Distance Formula]:
   `\displaystyle d = √((14 - 2)^2 + (1 - 10)^2)`
2. [Order of Operations] Evaluate:
   `\displaystyle d = 15`