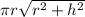Question

The formula for the lateral area of a right cone la=pirs, where r is the radius of the base and s is the slant height of the cone. which are equivalent equations?

Answer 1

A And D

Explanation:

Did The Quiz and got it right

Answer 2

`\pi r √(r^2+h^2)`

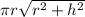
Explanation:

Given that there is a cone with radius r and slant height s.

We know that lateral surface area of the cone is

=
`\pi r s`

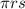
Alternately if instead of s, h is known we can write this in terms of h also.

Consider the right triangle formed by slant height, height and radius of the cone.

Using Pythagorean theorem we have

`s^2=r^2+h^2`

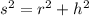
Or
`s=√(r^2+h^2)`

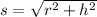
Hence lateral surface area of the cone

=
`\pi r √(r^2+h^2)`