Question

Which equation represents a parabola with a focus at (0,-2) and a directrix of y=6?

Answer 1

Hey there!!

First, let's learn the parabola formula when the focus and the directrix is given.

Formula :

`y = (( x - a ) ^(2) )/( 2 ( b - k ) ) + (( b + k ) )/(2)`

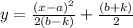
We have ,

Focus : ( 0 , -2 )

Hence, a = 0 and b = -2

And k = 6

Now, we will just have to plug in the values and find out the equation.

`y = (( x - 0 )^(2) )/(2 ( - 2 - 6 )) + (( - 2 + 6 ) )/(2)`

`y = (x^(2) )/(-16)+ 2`

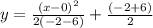
The final equation would be :

`y = (-x^(2) )/(16) + 2`

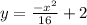
Hope my answer helps!!

Answer 2

Solution:
Any point (x,y) on the parabola is equidistant from the directrix and the focus:
Thus,
√[(x-0)²+(y-(-2))²]=y-(6)
√(x²+(y+2)²)=y-6
x²+(y+2)²=(y-6)²
x²+y²+4y+4=y²-12y+36
x²=-16y+32
x²=16(2-y)