Answer: A and D are the correct statements.
1. In ΔBRS and ΔBDC
∠R=∠D and ∠S=∠C [∵ corresponding angles]
So by AA similarity criteria ,
△BCD is similar to △BSR.
2. As RS is parallel to DS then by basic proportionality theorem,
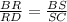
⇒ B is not true.
3. As we can see BC is greater than BS ,so it cannot possible.
If
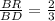 and
and

where BS=6 then
 .
.
4. As RS is parallel to DS then by basic proportionality theorem,
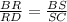
⇒BR×SC=RD×BS.
5. From 4 its not true that BR/RS = BS/SC.