The sum of the squares of two numbers is 18. the product of the two numbers is 9. find the numbers.

Question

asked Feb 12, 2019 9.8k views

2 Answers

Klenwell · Answer 1 · 2019-02-13T09:51:02+0000

Answer:

x=3 y=3

Explanation:

The sum of the squares of two numbers is 18, and the product of those two numbers is 9, you just need to create an equation:

So the sum of the squares is 18, the first number will be represented as X and the second as Y:

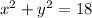
x^(2)+ y^(2) =18

And the other one is that the product of the two numbers is 9:

xy=9

We have a system of equations here, we clear X from the first one:

x=(9)/(y)

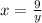
And instert that value of x in the first one:

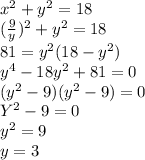
$x^(2)+ y^(2) =18\\((9)/(y) )^(2)+ y^(2) =18\\81=y^2(18-y^2)\\y^4-18y^2+81=0\\(y^2-9)(y^2-9)=0\\Y^2-9=0\\y^2=9\\y=3$

By solving this equation we get that the first number is 3.

The second number is solved by inserting the value of Y into one of the equations, in this case we will use the second:

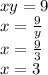
$xy=9\\x=(9)/(y) \\x=(9)/(3) \\x=3$

So we get that x and y are both 3.