Question

The athlete’s salary, in thousands, for the first two years is $400 and $400(1.05). Explain how to find her salary for each of the next three years. Do these values form a geometric sequence? Explain.

Answer 1

Edge Checklist:

Find the third year’s salary by multiplying the second year’s salary by 1.05

Find the fourth year’s salary by multiplying the third year’s salary by 1.05.

Find the fifth year’s salary by multiplying the fourth year’s salary by 1.05.

The salaries form a geometric sequence because the athlete’s salary changes by a common ratio of 1.05 each year.

Answer 2

To find the salary for the next three years, we are going to use the formula for the nth term of a geometric sequence:
`a_(n)=a_(1)r^(n-1)`
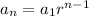
where

`a_(n)` is the nth term of the sequence

`a_(1)` is the first term in the sequence

`r` is the common ratio

`n` is the position of the term in the sequence

To check if the values $400 and 400(1.05) for a geometric sequence, we are going to find their common ratio. To find the common ratio, we are going to use the formula
`r= (a_(n) )/(a_(n-1))`
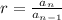
where

`a_(n)` is the current term in the sequence

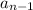
`a_(n-1)` is the previous term in the sequence

We can infer from our values, that the current term of the sequence is 400(1.5), so
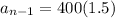
`a_(n-1)=400(1.5)`. That leaves 400 as the previous term, so
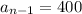
`a_(n-1)=400`. Lets replace those values in our formula to find
`r`:

`r= (a_(n) )/(a_(n-1))`

`r= (400(1.05))/(400)`

`r=1.05`

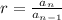
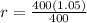
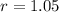
Now that we have our common ratio, we can replace it in our formula for the nth term to find the athlete's salary for each of the next three years. Notice that the first term of our sequence is $400, so
`a_(1)=400`

`a_(n)=a_(1)r^(n-1)`

`a_(n)=400(1.05)^(n-1)`

`a_(3)=400(1.05)^(3-1)`

`a_(3)=400(1.05)^(2)`

`a_(3)=441`


`a_(4)=400(1.05)^(4-1)`

`a_(4)=400(1.05)^(3)`

`a_(4)=463.05`


`a_(5)=400(1.05)^(5-4)`

`a_(5)=400(1.05)^4`

`a_(5)=486.2025`

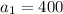
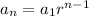
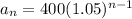
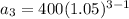
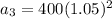
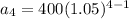
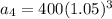
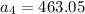
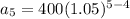
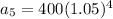
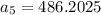
We can conclude that the athlete's salary for each of the next three years is: $441,$463.05,486.2025 respectively. Also, those vales for a geometric sequence because they share a common ratio, (1.05).