Question

The sum of the squares of two consecutive odd positive integers is 74. Find the integers.

Answer 1

Let’s use a sample set.
Let’s use 5 and 7.
5•5=25
7•7=49
49+25=74
The integers are 5 and 7. The way I found this was by thinking of 9 and 11 at first. I knew that it would be entirely way too much, but 3 and 1 would be too little. 5 and 7 fit in the middle of those two samples.

Your answer is 5 and 7.

Answer 2

Let first odd number be x

Then that would be
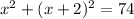
`x^2 + (x+2)^2=74`. We need to solve for x.


`x^2 + (x+2)^2=74\\\ \\x^2 + x^2 + 4x+4 = 74\\\ \\2x^2 + 4x +4=74\\\ \\2x^2+4x-70 = 0\\\ \\2(x^2+2x-35)=0\\\ \\2(x+7)(x-5)=0\\\ \\x=-7\text{ or }5`

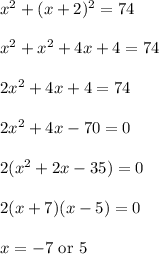
But we need positive integers so we would have
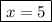
`\boxed{x=5}`, so then our integers would be x, x+2 = 5, 7

Check work:

5² + 7² = 25 + 49 = 74.

So our integers would be 5 and 7.

Hope this helps.