Question

In the diagram below what is the approximate length of the minor arc XY

Answer 1

The answer is B.

The formula for arc length is s = r(theta) Theta must be in radians, so convert 40 degrees to radians, which is 2pi/9. Multiply 2pi/9 by the radius, 9, and then you'll get the answer. Hopes this helps!

Answer 2

B. 6.3 cm

Step by step explanation:

We have been given measure of central angle which intercepts to our minor arc XY.

Since we know that the formula to find measure of arc length is:

`\text{Arc length}=(\theta)/(360)* \text{circumference of circle}`

`\text{Arc length}=(\theta)/(360)* {2\pi r}`

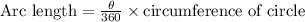
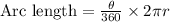
Now let us substitute our given values in above formula.

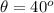`\theta=40^(o)` and
`radius=9 cm`

`\text{Arc length}=(40)/(360)* {2\pi \cdot 9}`

`\text{Arc length}=(1)/(9)* {2\pi \cdot 9}`

`\text{Arc length}=2 \pi`

`\text{Arc length}=6.2831853071795865\approx 6.3`

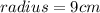
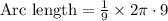
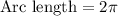
Therefore, length of minor arc XY is 6.3 cm and option B is the correct choice.