Question

Aisha wants to make two quilts, each with the same area. The first quilt will be square with sides s feet long. The second quilt will be a rectangle with a width that is half the length of a side of the square quilt and a length that is 6 feet longer than a side length of the square quilt. Which quadratic equation can be used to find s, the side length of the square quilt?

s^2 =(1/2s) (s + 6)
s^2 = (s)(s + 6)
s^2 =(1/2s) (6s)
s^2 = (s)(6s)

Answer 1

Option 1 -
`s^2=((1)/(2)s)(s+6)`

Explanation:

Given : Aisha wants to make two quilts, each with the same area. The first quilt will be square with sides s feet long. The second quilt will be a rectangle with a width that is half the length of a side of the square quilt and a length that is 6 feet longer than a side length of the square quilt.

To find : Which quadratic equation can be used to find s, the side length of the square quilt?

Solution :

The first quilt will be square,

Let the side of square be s

The area of the square is
`A=s* s`

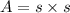
The second quilt will be a rectangle,

A width that is half the length of a side of the square quilt and a length that is 6 feet longer than a side length of the square quilt.

Width of the rectangle =
`(1)/(2)s`

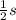
Length of the rectangle = s+6

Area of the rectangle is
`A=((1)/(2)s) * (s+6)`

According to question,

Area of square and rectangle are equal,

So,
`s* s=((1)/(2)s) * (s+6)`

`s^2=((1)/(2)s)(s+6)`

Therefore, Option 1 is correct.

The required equation is
`s^2=((1)/(2)s)(s+6)`

Answer 2

Sides of a square shape = S

Then, Area (A) = S^2

Width of rectangular shape = S/2
Length of rectangular shape = S+6

Then, Area (A) = (1/2S)(S+6)

The two area are equal. Therefore,
S^2 = (1/2S)(S+6)

The first option is the correct quadratic equation to solve for S.