Answer:
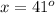
Explanation:
We have been given an equation
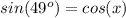 and we are asked to find the value of x.
and we are asked to find the value of x.
Since we know that trigonometric ratios are applied to right triangles and we also know that
 , where a and b are the angles other than 90 degree angle.
, where a and b are the angles other than 90 degree angle.
As one angle of our triangle is given 49 degrees, so to find the value of angle x we need to subtract 49 degrees from 90 degree angle as 49 degree angle and x will be equal to 90 degrees.
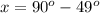
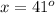
Therefore, the value of x is 41 degrees.