Question

For a function p(x)= x^2-9, what is the inverse function for the domain [0, infinity\

Answer 1

An inverse function is a function that reverses another function, so we have a function called:


`p(x)`

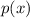
Then, the inverse function will be as follows:


`p^(-1)(x)`

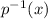
Given that
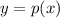
`y = p(x)`, we need to isolate x in terms of y:


`y = x^(2) -9`
∴
`y+9 = x^(2)`

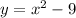
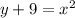
So:


`x=+√(y+9)` and
`x=-√(y+9)`

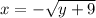
therefore, exchanging variables x and y:


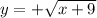
`y=+√(x+9)` and
`y=-√(x+9)`

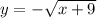
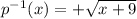
`p^(-1)(x)=+√(x+9)` and
`p^(-1)(x)=-√(x+9)`

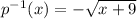
Which are the figures shown below.