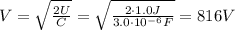Question

To what potential should you charge a 3.0 μf capacitor to store 1.0 j of energy?

Answer 1

The energy stored in a capacitor is given by:

`U= (1)/(2)CV^2`
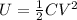
where
U is the energy
C is the capacitance
V is the potential difference

The capacitor in this problem has capacitance

`C=3.0 \mu F = 3.0 \cdot 10^(-6) F`
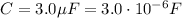
So if we re-arrange the previous equation, we can calculate the potential V that should be applied to the capacitor to store U=1.0 J of energy on it:

`V= \sqrt{ (2U)/(C) }= \sqrt{ (2 \cdot 1.0 J)/(3.0 \cdot 10^(-6)F) }=816 V`