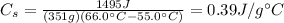Question

If 1495 j of heat is needed to raise the temperature of a 351 g sample of a metal from 55.0°c to 66.0°c, what is the specific heat capacity of the metal?

Answer 1

sorry i don't know the answer i'm really sorry

Answer 2

The amount of heat needed to increase the temperature of a substance by
`\Delta T` is given by

`Q= mC_s \Delta T`
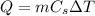
where m is the mass of the substance, Cs is its specific heat capacity and
`\Delta T` is the increase of temperature.

If we re-arrange the formula, we get

`C_s = (Q)/(m \Delta T)`
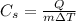
And if we plug the data of the problem into the equation, we can find the specific heat capacity of the substance:

`C_s = (1495 J)/((351 g)(66.0^(\circ)C-55.0^(\circ)C))=0.39 J/g^(\circ)C`