Question

If a hydrogen atom in the ground state absorbs a photon of energy 12.09 ev, to which state will the electron make a transition?

Answer 1

The energy levels of the hydrogen atom are given by

`E_n = -13.6 (1)/(n^2) [eV]` (1)
where n is the level number. Therefore, the ground state has energy of

`E_1 = -13.6 (1)/(1^2) eV = -13.6 eV`

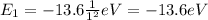
If the atom absorbs a photon of energy
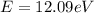
`E=12.09 eV`, the final energy of the hydrogen atom is

`E_f = E_1 + E = -13.6 eV + 12.09 eV =-1.51 eV`

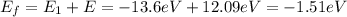
And we can use eq.(1) to find the corresponding level number:

`n= \sqrt{ (-13.6 eV)/(E_f) } = \sqrt{ (-13.6 eV)/(-1.51 eV)}= √(9)=3`
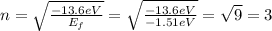
So, the electron made a transition to the n=3 level.