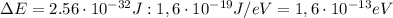Question

A relatively long lived excited state of an atom has a lifetime of 2.05 ms. what is the minimum uncertainty (in ev) in its energy?

Answer 1

We can solve the exercise by using Heisenberg's principle. In its energy-time version, Heisenberg principle states that the product between the uncertainty on the energy and on the time is larger than:

`\Delta E \Delta t \ \textgreater \ (h)/(4 \pi)` (1)
where
`\Delta E, \Delta t` are the uncertainties on the energy and on the time, and h is the Planck constant.

The lifetime of the particle is 2.05 ms, so we can assume the maximum uncertainty on the time corresponds to the lifetime itself:

`\Delta t = 2.05 ms = 2.05 \cdot 10^(-3) s`
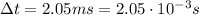
And so the minimum uncertainty on the energy can be found by using (1):

`\Delta E \ \textgreater \ (h)/(4 \pi \Delta t)= (6.6 \cdot 10^(-34) Js)/(4 \pi (2.05 \cdot 10^(-3) s))= 2.56 \cdot 10^(-32) J`

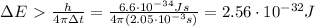
Keeping in mind that
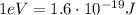
`1 eV = 1.6 \cdot 10^(-19)J`, we can convert the energy uncertainty into electronvolts:

`\Delta E = 2.56 \cdot 10^(-32) J : 1,6 \cdot 10^(-19) J/eV = 1,6 \cdot 10^(-13) eV`