Answer:
Option E is correct.
Explanation:
We have been two similar triangles and we are asked to find out the value of x.
Since we know that corresponding sides of similar triangles are in same ratio. We will set the ratio of corresponding sides to find out our x.
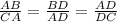
Now we will substitute our given values in this ratio.
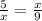
Now let us solve for x.
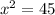
After taking the square root of both sides of the equation we will get,
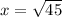
Therefore, option E is the correct choice.