Question

A satellite is in a circular orbit about the earth at a distance of one earth radius above the surface. what is the velocity of the satellite? (the radius of the earth is 6400 km and the mass of the earth is 5.98 * 1024 kg)

Answer 1

The gravitational attraction between the Earth and the satellite provides the centripetal force that keeps the satellite in circular motion:

`m (v^2)/(r)= G (Mm)/(r^2)`
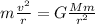
where
m is the satellite mass
v is its speed
r is its distance from the Earth's center
G is the gravitational constant
M is the Earth's mass

Re-arranging the formula, we get

`v= \sqrt{ (GM)/(r) }`

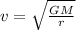
The satellite orbits at a distance equal to one Earth's radius (R) above the surface. This means that its distance from the Earth's center is twice the Earth radius:

`r=2R=2 \cdot 6400 km = 12800 km = 1.28 \cdot 10^4 m`

Therefore, its velocity is

`v= \sqrt{ (GM)/(r) }= \sqrt{ ((6.67 \cdot 10^(-11) m^3 kg^(-1) s^(-2))(5.98 \cdot 10^(24) kg))/(1.28 \cdot 10^4 m) }=1.76 \cdot 10^5 m/s`