Question

A monochromatic laser is exciting hydrogen atoms from the n=2 state to the n=5 state. part a what is the wavelength λ of the laser?

Answer 1

The energy levels of the hydrogen atom are given by

`E_n=-13.6 (1)/(n^2) [eV]`
where n is the level number.

In order to make transition from n=2 state to n=5 state, the electron should acquire an energy equal to the difference between the two energy levels:

`\Delta E= E_5 - E_2 = -13.6 (1)/(5^2)-(-13.6 (1)/(2^2))= -0.54+3.4=2.86 eV`

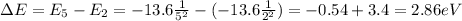
Keeping in mind that
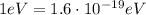
`1 eV = 1.6 \cdot 10^(-19)eV`, we can convert this energy in Joules

`\Delta E = 2.86 eV \cdot 1.6 \cdot 10^(-19) J/eV=4.58 \cdot 10^(-19) J`

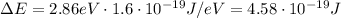
This is the energy the photons of the laser should have in order to excite electrons from n=2 state to n=5 state. Their frequency can be found by using

`\Delta E=hf`
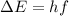
where h is the Planck constant and f is the photon frequency. Re-arranging it, we find

`f= (\Delta E)/(h)= (4.58 \cdot 10^(-19) J)/(6.6 \cdot 10^(-34) Js)=6.94 \cdot 10^(14) Hz`

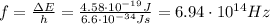
and finally we can use the relationship between frequency, wavelength and speed of light which holds for photons, in order to find their wavelength:

`\lambda= (c)/(f)= (3 \cdot 10^8 m/s)/(6.94 \cdot 10^(14) Hz)=4.32 \cdot 10^(-7) m =432 nm`
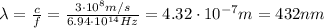
and this is the laser wavelenghth.