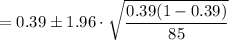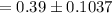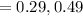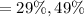Answer:
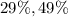
Explanation:
A recent poll of 85 randomly selected cable subscribers found that 39% would be willing to pay extra for a new nature channel.
Here,
p = proportion= 39% = 0.39,
n = sample size = 85,
Now we have to construct a 95% confidence interval for the proportion.
Confidence interval can be calculated by,
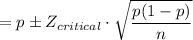
Putting the values,