Answer:
The complement of
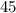 is
is
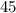 .
.
Explanation:
Method 1
From the isosceles right triangle; See diagram in attachment.
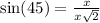

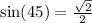
Also;
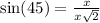
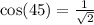
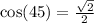
Hence;
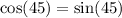
Method 2
 because the complement of
because the complement of
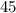 is still
is still
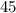 .
.
Complementary angles add to
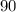 .
.
In general if we have an angle
 , then its complement is
, then its complement is
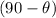 .
.
There is a relationship between the sine of an angle,
 and the cosine of its complement,(90-\theta)\degree[/tex].
and the cosine of its complement,(90-\theta)\degree[/tex].
The relationship is that,
 .
.
If
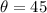 , then
, then
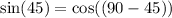 .
.
 .
.