Answer:
The measure of arc is 216°
Explanation:
Length of arc, L = 12π inches
Radius of the circle, R = 10 inches
Formula:
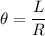
Where,
 in radian.
in radian.
By substituting L and R into formula.
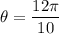

Now we change radian to degree
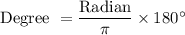
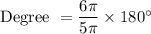
Central angle = 216°
Hence, The measure of arc is 216°