Answer:
Option 2 -

Explanation:
Given : The radius of one sphere is twice as great as the radius of a second sphere.
To find : The ratio of their surface areas?
Solution :
The surface area of the sphere is
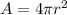
Let, the radius of one sphere is r
The surface area of one sphere is
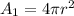
Radius of second sphere is R
The surface area of second sphere is
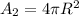
According to question,
The radius of one sphere is twice as great as the radius of a second sphere.
i.e, r=2R
Now, The ratio of their surface areas is
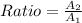
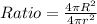
Substitute r=2R,
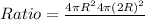
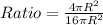
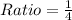
Therefore, Option 2 is correct.
The ratio of their surface area is
