Question

Find the value of the lesser root of x^2-6x+8=0

Answer 1

x² - 6x +8= 0,


`x= \frac{-b+/- \sqrt{b^(2)-4ac} }{2a} a=1, b=-6, c=8`


`x= (6+/- √(36-4*1*8) )/(2*1) x=(6+/- √(36-32) )/2 x=(6+/-2)/2 x_(1) =4, x_(2)=2`

Answer 2

The value of lesser root is:

x=2

Explanation:

We are given a quadratic equation in terms of variable " x " as:

`x^2-6x+8=0`

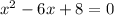
We know that for any quadratic equation of the type:

`ax^2+bx+c=0`

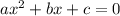
The roots of x are calculated as:

`x=(-b\pm √(b^2-4ac))/(2a)`

Here we have:

a=1 , b=-6 and c=8

Hence, on solving for roots:

`x=(-(-6)\pm √((-6)^2-4* 1* 8))/(2* 1)\\\\\\x=(6\pm √(36-32))/(2)\\\\\\x=(6\pm √(4))/(2)\\\\\\x=(6\pm 2)/(2)`

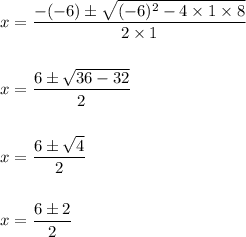
Hence, we have:

`x=(6+2)/(2)\ or\ x=(6-2)/(2)\\\\x=(8)/(2)\ or\ x=(4)/(2)\\\\\\x=4\ or\ x=2`

Hence, the value of lesser root is:

x=2