Answer:
0.835 mg of a 2.000-mg sample remains after 6.55 years.
Explanation:
We are given that The half-life of cobalt-60 is 5.20 yr.
Formula of half life :

Where N(0) = Initial amount
N(t) = Quantity remaining after time
t = time
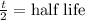
So, N(0) = Initial amount = 2 mg
t = time = 6.55 years
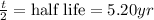
Substitute the values in the formula
Therefore,
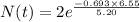
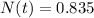
Hence 0.835 mg of a 2.000-mg sample remains after 6.55 years.