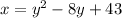Question

The vertex for of the equation of a parabola is x = ( y - 4 )2 + 27 what is the standard form

Answer 1

Important: indicate exponentiation with " ^ "

Thus, x = ( y - 4 )2 + 27 becomes x = ( y - 4 )^2 + 27

This can be re-written as x = y^2 - 8y + 16 + 27, or x = ay^2 - 8y + 43. This is the equation of the parabola in standard form x = ay^2 + by + c.

Answer 2

The standard form of this equation is

`x = y^(2) - 8y + 43`

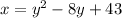
Explanation:

The exercise is asking us to convert the given equation to the standard form. Our goal is to get an expression like the one below...

`x = ay^(2) + by + c`

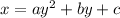
Now, let's work with the given parabola...

`x = (y - 4)^(2) + 27`

We can apply the Square of the Binomial formula
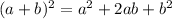`(a + b)^(2) = a^(2) + 2ab + b^(2)` to expand
`(y - 4)^(2)`

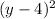
Then, we get

`x = y^(2) + 2y(-4) + (-4)^(2) + 27`

This can be simplified to

`x = y^(2) - 8y + 16 + 27`

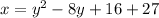
Finally, we can add number together

`x = y^(2) - 8y + 43`