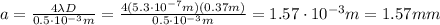Question

The distance between the first and fifth minima of a single-slit diffraction pattern is 0.500 mm with the screen 37.0 cm away from the slit, when light of wavelength 530 nm is used. find the slit width.

Answer 1

In the single-slit experiment, the displacement of the minima of the diffraction pattern on the screen is given by

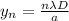
`y_n= (n \lambda D)/(a)` (1)
where
n is the order of the minimum
y is the displacement of the nth-minimum from the center of the diffraction pattern

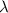
`\lambda` is the light's wavelength
D is the distance of the screen from the slit
a is the width of the slit

In our problem,

`D=37.0 cm=0.37 m`

`\lambda=530 nm=5.3 \cdot 10^(-7) m`
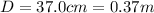
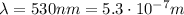
while the distance between the first and the fifth minima is

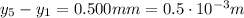
`y_5-y_1 = 0.500 mm=0.5 \cdot 10^(-3) m` (2)

If we use the formula to rewrite
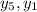
`y_5, y_1`, eq.(2) becomes

`(5 \lambda D)/(a) - (1 \lambda D)/(a) =(4 \lambda D)/(a)= 0.5 \cdot 10^(-3) m`
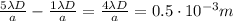
Which we can solve to find a, the width of the slit:

`a= (4 \lambda D)/(0.5 \cdot 10^(-3) m)= (4 (5.3 \cdot 10^(-7) m)(0.37 m))/(0.5 \cdot 10^(-3) m)= 1.57 \cdot 10^(-3) m=1.57 mm`