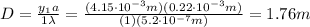Question

Light of wavelength 520 nm passes through a slit of width 0.220 mm. (a) the width of the central maximum on a screen is 8.30 mm. how far is the screen from the slit?

Answer 1

In the single-slit experiment, the displacement of the minima of the diffraction pattern on the screen is given by

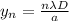
`y_n= (n \lambda D)/(a)` (1)
where
n is the order of the minimum
y is the displacement of the nth-minimum from the center of the diffraction pattern

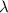
`\lambda` is the light's wavelength
D is the distance of the screen from the slit
a is the width of the slit

In our problem,

`\lambda=520 nm=5.2 \cdot 10^(-7) m`

`a=0.22 mm=0.22 \cdot 10^(-3) m`
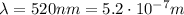
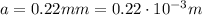
while the width of the central maximum on the screen corresponds to twice the distance of the first minimum from the center, and it is equal to

`2 y_1 = 8.30 mm=8.3 \cdot 10^(-3) m`
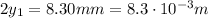
Therefore the distance of the first minimum from the center is

`y_1 = (8.3 \cdot 10^(-3) m)/(2)=4.15 \cdot 10^(-3) m`

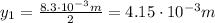
If we plug these numbers into eq.(1), we can find D, the distance of the screen from the slit:

`D= (y_1 a)/( 1 \lambda )= ((4.15 \cdot 10^(-3) m)(0.22 \cdot 10^(-3) m))/((1)(5.2 \cdot 10^(-7) m))= 1.76 m`