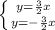This is the case of parametric derivatives in which x and y are expressed as functions of a variable t.
The first derivative implies that:
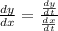
So we need to find both derivatives as functions of the variable t, then:
![(dy)/(dt) = 3[cos(t)cos(t)+sin(t)(-sin(t))]](https://img.qammunity.org/2019/formulas/mathematics/college/v2gc09rpha3zlii90od3mpadvvf69nzyyj.png)
![(dy)/(dt) = 3[cos^(2) (t)-sin^(2) (t)]](https://img.qammunity.org/2019/formulas/mathematics/college/iaskwbmw0ah2vv6vq3ylxnade1gsp1irof.png)
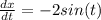
Thus:
![(dy)/(dx) = (-3[cos^(2) (t)-sin^(2) (t)])/(2sin(t))](https://img.qammunity.org/2019/formulas/mathematics/college/10mnls9sxx3v26vczcwy1roedux2p19fd3.png)
At (0,0)

and
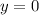
, so:

∴
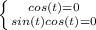
There are two values between -π and π which satisfy these equations simultaneously, namely:
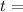
π/2
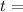
-π/2
The equation of a straight line given a point and its slope is
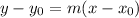
Given that the point is (0,0), then the equation can be written as:

So we will find two straight lines:
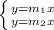
For

:
![m_(1)= (dy)/(dx) = (-3[cos^(2) ( \pi /2)-sin^(2) ( \pi /2)])/(2sin( \pi /2)) = (3)/(2)](https://img.qammunity.org/2019/formulas/mathematics/college/tqq5amnscjl6an3v71p4z510bfjv7q6u7w.png)
For
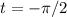
:
![m_(2)= (dy)/(dx) = (-3[cos^(2) ( -\pi /2)-sin^(2) ( -\pi /2)])/(2sin(- \pi /2)) = -(3)/(2)](https://img.qammunity.org/2019/formulas/mathematics/college/hp8rw4oyinnjnw3hj9xzkwyqlr96awf9rr.png)
Lastly: