Question

Which statement best describes the domain and range of f(x) = –(7)x and g(x) = 7x?

Answer 1

all real #s for both of em

Explanation:

you're welcome

Answer 2

First of all, A function
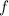
`f` from a set
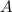
`A` to a set
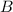
`B` is a relation that assigns to each element
`x` in the set
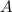
`A` exactly one element in the set [/tex]B[/tex]. The set
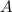
`A` is the domain (or set of inputs) of the function and the set
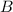
`B` contains the range (or set of outputs).

First.


`f(x)=-7x`

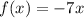
The graph of this equation is shown in Figure 1. As you can see this is a straight line with negative slope and does not intersect the y-axis.

So the statement that best describes this problem is:

Both the domain and the range is the set of all real numbers.

Second


`g(x)=7x`

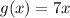
The graph of this equation is shown in Figure 2.This is also a straight line but it has positive slope. This one does not intersect the y-axis either.

So the statement that best describes this problem is:

Both the domain and the range is the set of all real numbers.