Answer: 13
Explanation:
Given : The equation
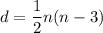 gives the number of diagonals d for polygon with n sides.
gives the number of diagonals d for polygon with n sides.
To find the number of sides n for a polygon that has 65 diagonals, we substitute the value of d= 65 in the given equation, we get

Multiply 2 on both sides , we get
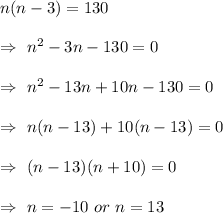
But number of sides cannot be negative, so the number of sides n for a polygon that has 65 diagonals = 13