Answer:
(–3, 6) and (6, –9) and (0, 2) and (5, 5)
Explanation:
Given : Slope =
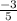 .
.
To find: Which ordered pairs could be points on a line that is perpendicular to this line.
Solution : We have given that Slope =
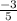 .
.
Slope =
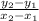 .
.
For (–8, 8) and (2, 2)
Slope =
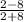 .
.
Slope =
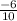 .
.
Slope =
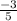 .
.
For (–5, –1) and (0, 2).
Slope =
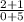 .
.
Slope =
 .
.
For, (–3, 6) and (6, –9)
Slope =
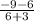 .
.
Slope =
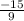 .
.
Slope =
 .
.
For (–2, 1) and (3, –2)
Slope =
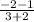 .
.
Slope =
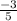 .
.
For (0, 2) and (5, 5)
Slope =
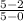 .
.
Slope =
 .
.
Therefore, (–3, 6) and (6, –9) and (0, 2) and (5, 5)