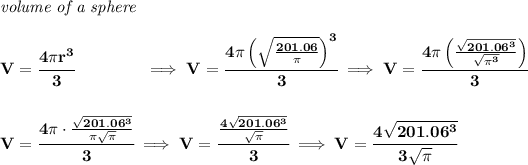
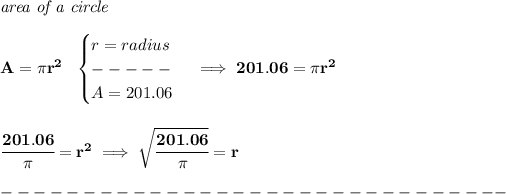assuming you meant a "circular cross-section" of 201.06 in².
so, we know if we cut the sphere like a cantaloupe, in half, the circular inner-part of the cantaloupe will have an area of 201.6 in².
keeping in mind that, the radius of that circular section, is the same radius of the sphere, what is it anyway?