Question

Calculating Orbital Period The Hubble Space Telescope (HST) orbits 569 km above Earth’s surface. If HST has a tangential speed of 7,750 m/s, how long is HST’s orbital period? The radius of Earth is 6.38 × 106 m.

Answer 1

The answer is, 5630 seconds.

Answer 2

Orbital period, T = 93.89 minutes

Step-by-step explanation:

It is given that,

The tangential speed of the Hubble Space Telescope, v = 7750 m/s

The radius of earth,
`r=6.38* 10^6\ m`

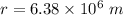
We need to find the orbital period of the Hubble Space Telescope that orbits 569 km above the Earth's surface i.e. h = 569 km = 569000 m

The orbital speed is given by,

`v=(2\pi R)/(T)`

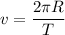
T is the orbital period

R = r + h

R = 6949000 m

`T=(2\pi R)/(v)`

`T=(2\pi * 6949000\ m)/(7750\ m/s)`

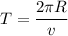
T = 5633.78 s

or

T = 93.89 minutes

So, the orbital period of the Hubble Space Telescope is 93.89 minutes. Hence, this is the required solution.