The volume of a pyramid with a square base is given by:
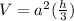
. This is the way the volume is usually given but we can also multiply the two terms and write it this way:
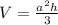
.
We are looking to triple the Volume which means we want to multiply it by 3. With respect to our volume equation, we multiply both sides by 3 to obtain:
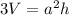
So, we are looking to see which of the choices given produces a volume equal to

.
The first choice is the right answer. Notice what happens when we take the volume formula and multiply the h by 3. We get:
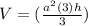
and since there is a 3 in both the numerator (top) and the denominator (bottom) we can cross these out. That leaves us with a volume equal to

which is what we were looking for!