Question

Please help! i dont understand this.

a 25 gram sample substance that's used for drug research has a k-value of 0.1229. find the substances half-life, in days using the exponential decay formula. round your answer to the nearest tenth

Answer 1

instead of using 0.41No you use 0.5No. rearranging the same way gives you t=(ln0.5)/(-k)=5.5 to the nearest 10th

Answer 2

Half life period = 43.11 days

Explanation:

A sample substance has been taken for the use of drug research.

Weight of the substance taken = 0.25 gram

We have to use the formula of exponential decay to find the half life period of the substance.

Formula for the decay is
`A_(t)=A_(0)e^(-kt)`

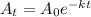
Where
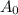`A_(0)` is the weight of the substance taken initially

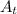`A_(t)` is the quantity remained after t time

and t = time

Now we have to find the half life life period

`A_(t)` =
`(0.25)/(2)=.0125`

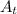and
`A_(0)=25`

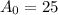
By putting these values in the formula

0.125 = 25
`e^(-0.1229t)`

`e^(-0.1229t)` =
`(0.125)/(25)`

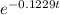
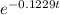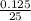
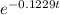`e^(-0.1229t)` = 0.005

Now we take natural log on both the sides of the equation

`ln(e^(-0.1229t))=ln(.005)`

-0.1229t(lne) = -5.2983

0.1229t = 5.2983

t =
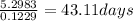`(5.2983)/(0.1229)=43.11 days`≈ 43.10 days

Therefore, half life period of the substance is 43.10 days