Question

What is the measure, in degrees, of the angle marked B?

133

65

68

47

Answer 1

47

All triangles are 180 degrees. Add the 2 numbers given to get a number. Take 180 and subtract it from that number to get 47

Answer 2

`\boxed {\boxed {\sf 133 \ degrees }}`

Explanation:

According to the Exterior Angle Theorem, the exterior angle of a triangle is equal to the sum of the 2 remote and opposite interior angle.

`d=a+b`

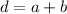
In this triangle, angle B is the exterior angle (d). The two interior angles are 68 degrees and 65 degrees ( a and b).

`\angle B=68 \textdegree +65 \textdegree`

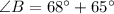
Add.

`\angle B= 133 \textdegree`

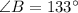
This can also be solved using triangles and supplementary angles.

The angles in a triangle must add to 180 degrees. We have three angles: 68, 65, and an unlabeled angle we can call x.

`68+65+x=180 \\133+x=180`

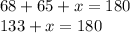
Subtract x from both sides.

`133+x=180-133 \\x=47`

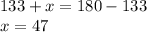
x is on a straight line with B, so they are supplementary and add to 180 degrees.

`47+ \angle B= 180`

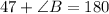
Subtract 47 from both sides.

`47-47+ \angle B= 180-47\\\angle B= 133`

Angle B is equal to 133 degrees.