Question

Find the area of ΔAOB

3√3 un2
4.5√3 un2
9√3 un2

Answer 1

9√3 un2

Explanation:

i just did the assignment

Answer 2

The area of the ΔAOB is
`9√(3)\ unit^(2)` .

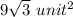Explanation:

As given the figure

OA = OB = 6 unit

(Radius of the circle.)

In ΔAOB

As the two sides of a triangle thus there opposite angles are also equal .

∠A = ∠B

Let us assume that ∠A = ∠B = x°

∠A + ∠O + ∠B = 180°

(By using the angle sum property of a triangle.)

∠O = 60°

x° + 60° + x° = 180°

2x = 180 - 60

2x = 120

`x = (120)/(2)`

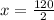
x = 60

∠A = ∠B = 60°

Thus

∠A = ∠B = ∠O = 60°

As all the angles of the ΔAOB are 60° thus ΔAOB is a equilateral triangle .

Also all the sides of the ΔAOB are also equal i.e AB = OA = OB = 6 unit .

Formula

`Area\ of \ a\ equilateral\ triangle = (√(3))/(4) a^(2)`

Where a is the side of the equilateral triangle .

a = 6 unit

Put in the above formula

`Area\ of \ a\ equilateral\ triangle = (√(3))/(4)* 6^(2)`

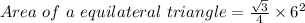
6² = 36

`Area\ of \ a\ equilateral\ triangle = (√(3))/(4)* 36`

`Area\ of \ a\ equilateral\ triangle = 9√(3)\ unit^(2)`

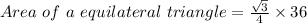
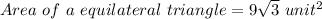
Therefore the area of the ΔAOB is
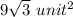`9√(3)\ unit^(2)` .