Answer:
Option B is correct
The minimum number of pens the company must sell to make a profit is, 174.
Step-by-step explanation:
Let x be the number of pens and y be the cost of the pens.
To find the cost of the equation.
It is given that cost , y , of manufacturing the pens is a quadratic function i.,e
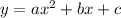 ......[1]
......[1]
and y-intercept of 120 which means that for x=0 , y=120 and Vertex = (250 , 370).
Put x = 0 and y =120 in [1]
120 = 0+0+c
⇒ c= 120.
Since, a quadratic function has axis of symmetry.
The axis of symmetry is given by:
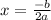 ......[2]
......[2]
Substitute the value of x = 250 in [2];
 or
or
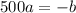 ......[3]
......[3]
Substitute the value of x=250, y =370, c =120 and b = -500 a in [1];
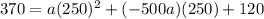 or
or
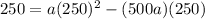 or
or
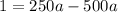
or
1 = -250 a
⇒
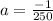
We put the value of a in [3]
So,
b =-500 a=
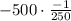
Simplify:
b =2
Therefore, the cost price of the pens is:
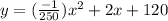
And the selling of the pens is 2x [ as company sell pens $ 2 each]
To find the minimum number of pens the company must sell to make a profit:
profit = selling price - cost price
Since to make minimum profit ; profit =0
then;
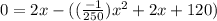 or
or

Simplify:
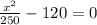
⇒
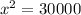 or
or
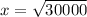
Simplify:
x =173.205081
or
x = 174 (approx)
Therefore, the minimum number of pens the company must sell to make a profit is, 174