A population of rodents becomes stranded on a remote island. Eventually, the population reaches the island’s carrying capacity. When this happens the population growth curve becomes flat as shown in the image. At this stage the change in population becomes zero with time. The logistic growth curve for the population growth is given by the formula,
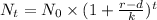
Where, r is the growth rate, d is the death rate, and k is the carrying capacity.
When,
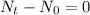
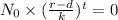
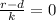
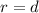
The growth rate equals the death rate of the rodents.
The answer is (A).