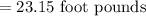Answer: The Work done to move the object is
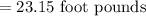
Explanation:
Given;
Force F=3
Vectors of F= (3,-1)
Moves object to a distance=9
Let A and B be the displacements Vectors
A= (0,-5)
B= (6,-2)
To Find:
Work done in foot-pounds
Solution:
Work done
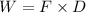
Direction of force vector= (3,-1) (i, j)
=3i-j
Unit of force vector

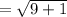
Force vector=(Force/Unit Vector)Direction of force vectors
F=
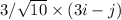
Direction of motion vector= (B-A)
= (6,-2)-(0,-5) x i,j)
=(6-0),(-2-5) x (i, j)
=(6,-7) x (i, j)
=6i-7j
Unit of motion vector
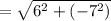
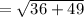
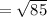
Motion Vector= (Distance moved by the object/Unit motion vector) × (Direction of motion vectors)
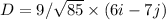
Workdone
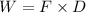
![= [3/ √(10) * (3i-j)] * [9/ √(85) * (6i-7j)]](https://img.qammunity.org/2019/formulas/mathematics/high-school/enthdc80orlthu6g6kshtnn3qwlzucnlh0.png)
![= [3/ √(10) * 9/ √(85)] * [(3i-j) *(6i-7j)]](https://img.qammunity.org/2019/formulas/mathematics/high-school/k7k69465mo72a9fj2oizmfzh5g95c2igxd.png)
![= [3/3.1623 * 9/9.2195] * [(3*6) + ((-1) * (-7))]](https://img.qammunity.org/2019/formulas/mathematics/high-school/30lw06cgj8k0s4jhl6so8etrdev20mgcap.png)
![= [0.94867 * 0.97619] * [18+7]](https://img.qammunity.org/2019/formulas/mathematics/high-school/dkgj9w965ys731ksrgas19saochujj820v.png)
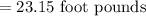
Result:
Work done to move an object