Answer:
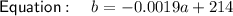
209.44 °F
Explanation:
Define the variables:
- a = altitude, in feet.
- b = boiling point, in degrees Fahrenheit.
Given:
- At an altitude of 8100 ft, the liquid boils at 198.61°F.
- At an altitude of 4500 ft, the liquid boils at 205.45°F.
If the relationship between altitude (a) and boiling point (b) is linear, this can be modelled as:
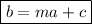
where:
- a is the independent variable.
- b is the dependent variable.
- c is a constant.
Find the slope of the linear equation by substituting the given ordered pairs into the slope formula:
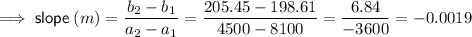
Substitute the found slope and one of the ordered pairs into the point-slope formula:
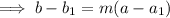
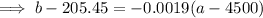

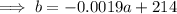
Therefore, an equation giving the boiling point (b) of the liquid in terms of altitude (a) is:
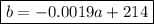
To find the boiling point of the liquid at 2400 ft, substitute a = 2400 into the found equation:
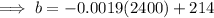
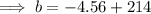
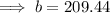
Therefore, the boiling point of the liquid at 2400 ft is 209.44 °F.