Question

The relationship between altitude and the boiling point of a liquid is linear. At an altitude of 8100 ​ft, the liquid boils at 198.61°F. At an altitude of 4500 ​ft, the liquid boils at 205.45°F. Write an equation giving the boiling point b of the​ liquid, in degrees​ Fahrenheit, in terms of altitude​ a, in feet. What is the boiling point of the liquid at 2400 ​ft?

Write an equation.
b=

Answer 1

What is the relationship between altitude and boiling point of a liquid?

At a higher elevation, the lower atmospheric pressure means heated water reaches its boiling point more quickly—i.e., at a lower temperature. Water at sea level boils at 212 degrees Fahrenheit; at 5,000 feet above sea level, the boiling point is 203 degrees F. Up at 10,000 feet, water boils at 194 degrees F.

Explanation:

Answer 2

`\textsf{Equation}: \quad b=-0.0019a+214`

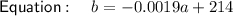
209.44 °F

Explanation:

Define the variables:

• a = altitude, in feet.
• b = boiling point, in degrees​ Fahrenheit.

Given:

• At an altitude of 8100 ​ft, the liquid boils at 198.61°F.
• At an altitude of 4500 ​ft, the liquid boils at 205.45°F.

If the relationship between altitude (a) and boiling point (b) is linear, this can be modelled as:

`\boxed{b=ma+c}`

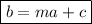
where:

• a is the independent variable.
• b is the dependent variable.
• c is a constant.

Find the slope of the linear equation by substituting the given ordered pairs into the slope formula:

`\implies \textsf{slope}\:(m)=(b_2-b_1)/(a_2-a_1)=(205.45-198.61)/(4500-8100)=(6.84)/(-3600)=-0.0019`

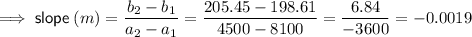
Substitute the found slope and one of the ordered pairs into the point-slope formula:

`\implies b-b_1=m(a-a_1)`

`\implies b-205.45=-0.0019(a-4500)`

`\implies b-205.45=-0.0019a+8.55`

`\implies b=-0.0019a+214`

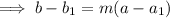
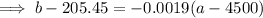
Therefore, an equation giving the boiling point (b) of the​ liquid in terms of altitude​ (a) is:

`\boxed{b=-0.0019a+214}`

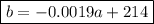
To find the boiling point of the liquid at 2400 ​ft, substitute a = 2400 into the found equation:

`\implies b=-0.0019(2400)+214`

`\implies b=-4.56+214`

`\implies b=209.44`

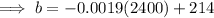
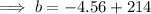
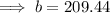
Therefore, the boiling point of the liquid at 2400 ft is 209.44 °F.