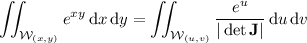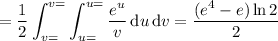Question

Evaluate the integral e^xy w region d xy=1, xy=4, x/y=1, x/y=2

Answer 1

Make a change of coordinates:


`u(x,y)=xy`

`v(x,y)=\frac xy`

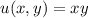
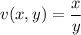
The Jacobian for this transformation is


`\mathbf J=\begin{bmatrix}(\partial u)/(\partial x)&(\partial v)/(\partial x)\\\\(\partial u)/(\partial y)&(\partial v)/(\partial y)\end{bmatrix}=\begin{bmatrix}y&x\\\\\frac1y&-\frac x{y^2}\end{bmatrix}`

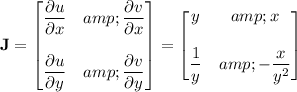
and has a determinant of


`\det\mathbf J=-\frac{2x}y`

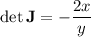
Note that we need to use the Jacobian in the other direction; that is, we've computed


`\mathbf J=(\partial(u,v))/(\partial(x,y))`

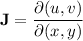
but we need the Jacobian determinant for the reverse transformation (from
`(x,y)` to
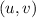
`(u,v)`. To do this, notice that


`(\partial(x,y))/(\partial(u,v))=\frac1{(\partial(u,v))/(\partial(x,y))}=\frac1{\mathbf J}`

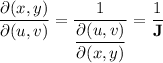
we need to take the reciprocal of the Jacobian above.

The integral then changes to


`\displaystyle\iint_{\mathcal W_((x,y))}e^(xy)\,\mathrm dx\,\mathrm dy=\iint_{\mathcal W_((u,v))}(e^u)/(|\det\mathbf J|)\,\mathrm du\,\mathrm dv`

`=\displaystyle\frac12\int_(v=)^(v=)\int_(u=)^(u=)\frac{e^u}v\,\mathrm du\,\mathrm dv=\frac{(e^4-e)\ln2}2`