Question

If the motor exerts a force of F = (600 + 2s2) N on the cable, determine the speed of the 100-kg crate when it rises to s = 15 m. The crate is initially at rest on the ground.

Answer 1

Speed of the 100 kg crate, v = 136 m/s

Step-by-step explanation:

It is given that,

Force exerted by a motor, F = (600+2 s²) N

mass of the crate, m = 100 kg

We have to find the speed of the crate. Force is given by the product of mass and acceleration.

F = m a

g is acceleration due to gravity

`F=m(d^2s)/(dt^2)`

`(d^2s)/(dt^2)=(600+2s^2)/(100)`

`(d^2s)/(dt^2)=6+0.02s^2`

`(d^2s)/(dt^2)-6-0.02s^2=0`

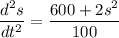
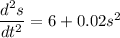
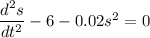
or

s"- 6 - 0.02 s² = 0

On solving the above differential equation using calculator with when initially the crate is at rest s(0) = 0 and s'(0) = 15 m

`s(t)=150\ e^(-√(2)t)+150\ e^(√(2)t)-300`

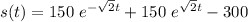
Differentiating above equation w.r.t t to get velocity of the crate.

So, v = 136 m/s

Hence, this is the required solution.

Answer 2

The motor that exerts force is F = 600+2s²
Mass of crate is m= 100kg
Distance raises is s= 15m
Crate at rest is V₁ =0
We will solve this using principle of energy and work because involves displacement, velocity, and force
Work energy is
T₁ +ΣU₁₋₂ = T₂
Whereby T₁ = initial Kinetic energy
= 1/2mw₁² = 1/2m(o)₁² = 0 Because initial is at rest.
Motor exerts the force on the cable forces acting in the cable at C are two times motor exerts force cable M work done by the exerted motor is
U₁₋₂ = 2∫s²Fds
U₁₋₂ = 2∫s²(600+2S²)ds
=2(600×s+ 2s³/3)¹⁵
= 2(600 ×15 + 2× 15³/3)
=22500N
Work done by crate is the crates' weight acts downward to take the negative sign
U₁₋₂ = -(m × g × s)
U₁₋₂ = -(100× 9.81 × 15)
= -14715N
T₂ = Final kinetic energy = 1/2mw²₂
T₁ +∑U₁₋₂ =T₂
0 + (22500 +(-14715)) = 1/2(100) V²₂
V₂ = 12.47m/s