Question

A sound from a source has an intensity of 270 dB when it is 1 m from the source.

What is the intensity of the sound when it is 3 m from the source?

30 dB
90 dB
810 dB
2430 dB

Answer 1

Remember that sound intensity decreases in inverse proportion to the distance squared. So, to solve this we are going to use the inverse square formula:
`(I_(2) )/(I_(1))= (\frac{d{2} }{d_(1)})^2`
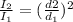
where

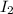
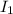
`I_(2)` is the intensity at distance 2

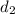
`I_(1)` is the intensity at distance 1

`d_(2)` is distance 2

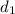
`d_(1)` is distance 1

We can infer for our problem that
`I_(1)=270`,
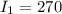
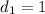
`d_(1)=1`, and
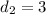
`d_(2)=3`. Lets replace those values in our formula to find
`I_(2)`:

`(I_(2) )/(I_(1))= (\frac{d{2} }{d_(1)})^2`

`(I_(2) )/(270) =( (1)/(3) )^2`

`(I_(2) )/(270) = (1)/(9)`

`I_(2)= (270)/(9)`

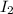
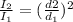
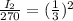
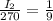
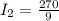
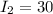
`I_(2)=30` dB

We can conclude that the intensity of the sound when is 3 m from the source is 30 dB.