2 Answers

BlueHula · Answer 1 · 2019-06-24T13:56:34+0000

For this case we have that by definition the constant of variation of a line is given by the slope m, of said line.

Where:

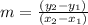
$m = \frac {(y_ {2} -y_ {1})} {(x_ {2} -x_ {1})}$

To find the slope of a line it is necessary to find two points through which the line passes.

To solve the given problem, we find the slopes of the lines shown in the graphics R and S:

Graphic R:

It is observed that the line passes through the following points:

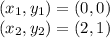
$(x_ {1}, y_ {1}) = (0,0)\\(x_ {2}, y_ {2}) = (2,1)$

Substituting in the formula of the slope we have:

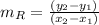
$m_ {R} = \frac {(y_ {2} -y_ {1})} {(x_ {2} -x_ {1})}$

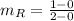
$m_ {R} = \frac {1-0} {2-0}$

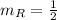
$m_ {R} = \frac {1} {2}$

Thus, the slope of the line of the graph R is given by:
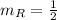
$m_ {R} = \frac {1} {2}$

Graphic S:

It is observed that the line passes through the following points:

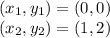
$(x_ {1}, y_ {1}) = (0,0)\\(x_ {2}, y_ {2}) = (1,2)$

Substituting in the formula of the slope we have:

$m_ {S} = \frac {(y_ {2} -y_ {1})} {(x_ {2} -x_ {1})}$

$m_ {S} = \frac {2-0} {1-0}$

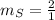
$m_ {S} = \frac {2} {1}$

$m_ {S} = 2$

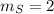
Thus, the slope of the line of the graph R is given by:
$m_ {S} = 2$

$m_ {S}> m_ {R}$

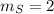
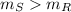
then, the graph S has a variation constant greater than the graph R.

Answer:

The graph S has a variation constant greater than the graph R.

Rachel's idea is wrong

Please log in or register to add a comment.