Question

120e^(2x)=75e^(3x)
Please solve with steps

Answer 1

Step 1. Take natural logarithm to both sides of the equation:

`120e^(2x)=75e^(3x)`

`ln(120e^(2x))=ln(75e^(3x))`

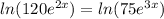Step 2. Apply product rule of logarithms
`ln(ab)=ln(a)+ln(b)`:

`ln(120)+ln(e^(2x))=ln(75)+ln(e^(3x))`

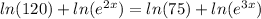Step 3. Apply the rule
`ln(e^x)=x`:

`ln(120)+2x=ln(75)+3x`

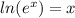
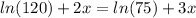Step 4. Solve for
`x`:

`ln(120)+2x=ln(75)+3x`

`ln(120)-ln(75)=3x-2x`

`x=ln(120)-ln(75)`
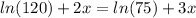
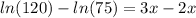
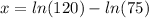
Apply the quotient rule of logarithms
`ln(a)-ln(b)= ln((a)/(b) )`:

`x=ln( (120)/(75) )`

`x=ln( (8)/(5) )`

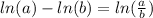
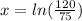
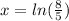We can conclude that the solution of our equation is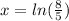
`x=ln( (8)/(5) )`, which is approximately
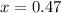
`x=0.47`.